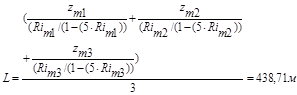Купцов А.И., Акберов Р.Р., Гимранов Ф.М., Зубков А.Г. «Определение параметров атмосферного пограничного слоя с целью моделирования сброса опасного газа и его последующего распространения в окружающей среде», — Научный журнал «Вестник технологического университета», №6— 2016, с. 114-119.
Ключевые слова: технологические свечи, рассеивание газа, численное моделирование.
Поэтапным использованием метода градиента и профиля определены параметры атмосферного пограничного слоя. Установлены профили скорости, температуры и характеристики турбулентности. Приведены расчеты сброса этилена через свечу при различных устойчивостях.
Keywords: technological candles, gas dispersion, numerical simulation.
In stages using a gradient method and the profile parameters of the atmospheric boundary layer is determined. Set speed profile, temperature and turbulence characteristics. Results ethylene relief payments through the candle at various sustainability.
На газоперерабатывающих и нефтехимических производствах на случай возникновения аварийной ситуации предусматриваются системы аварийного освобождения технологического оборудования от опасных паров и газов. При этом допускается непосредственный сброс легких газов в атмосферу, содержащихся в оборудовании, через свечу рассеивания. Сбросы газов могут также являться и регламентированной процедурой, выполняемой для освобождения технологического оборудования и трубопроводов перед проведением плановых ремонтных работ. В этом случае выбросы из свеч осуществляются, как правило, в течение относительно продолжительного периода времени и характеризуются плавным падением давления среды в опорожняемом оборудовании.
В настоящее время для проектирования свеч рассеивания используются инженерные методики [1,2], предназначенные для определения конструктивных и эксплуатационных параметров свечи: высоты, диаметра и приемлемого расхода сброса (кг/с), а также максимальной концентрации сбрасываемого газа в приземной области. Однако, аварии, произошедшие недавно на ООО «Томскнефтехим» [3], на газопроводе-подключении газоконденсатного месторождения Крайнего Севера [4] и на некоторых других объектах, а также эксперименты с выбросом природного газа [5] свидетельствуют о возможности создания у поверхности земли взрывоопасных концентраций газа. Из вышесказанного следует, что расчеты, выполняемые по инженерным методикам, не всегда способны корректно описывать реальные процессы пространственно-временного рассеивания газа, сбрасываемого со свечи. Анализ этих и некоторых других методик расчета распространения газов в атмосфере [6] показал, что в их основе лежат допущения и упрощенные зависимости, например:
— использование коэффициентов, аппроксимирующих определенную совокупность метеорологических факторов (так называемых классов устойчивости атмосферы);
— использование коэффициентов, учитывающих рельеф местности и наличие промышленной застройки на пути рассеивание газа;
— не учитывается нестационарность процесса опорожнения оборудования и принимается неизменным профиль скорости ветра во времени;
— допущение постоянства плотности сбрасываемого опасного газа и т.д.
В качестве альтернативы вышеупомянутым упрощенным инженерным методикам для расчетов распространения парогазовоздушных облаков в атмосфере стали активно применяться методики расчета [7-10], основанные на численном решении уравнений сохранения массы, количества движения, энергии и др. в комплексах прикладных программ (генератор расчетной сетки, решатель, визуализатор и т.д.).
Физико-математическая модель
Авторами, для решения задач, связанных с численным моделированием сброса газа через технологические свечи, применяется предложенная ими ранее физико-математическая модель [11]. В основе этой модели лежит система дифференциальных уравнений, определяющих трехмерный нестационарный поток газовоздушной смеси; перенос энергии, массы, турбулентной кинетической энергии и скорости диссипации турбулентной кинетической энергии. Ее главной особенностью является использование модифицированных констант турбулентности, источникового члена в уравнении переноса турбулентной кинетической энергии и итерационного метода получения однородного профиля давления для всей расчетной области. Фактически базис модели позволяет воспроизводить различные варианты устойчивости атмосферы с применением теории подобия Монина-Обухова.
Геометрия расчетной области для моделирования сброса представляет собой область правильной ортогональной формы, а ее пространственная дискретизация производится с использованием трехмерных элементов регулярной гексаэдральной формы. При выборе размеров расчетной области учитывалось то, что, с одной стороны, одним из граничных условий являлась нулевая концентрация сбрасываемого газа, а, с другой стороны, протяженность области в направлении распространения газа должна быть минимальна для сокращения времени вычисления. При создании подобной пространственной сетки особое внимание уделяется к областям вблизи свечи. В этих областях сетка, должна быть сгущена по направлению к свече, что сводит к минимуму ошибки численной аппроксимации уравнений. Пример построения сетки авторами приведен в работе [10].
После предварительного моделирования пограничного атмосферного слоя задается граничное начальное условие на оголовке свечи (источник сброса) в виде функций массового расхода или давления сбрасываемого газа (пара) от времени. Процедура и сам вид функциональной зависимости представлены в работе [12]. Решение системы уравнений в сопряженной постановке позволяет учесть эффект дросселирования в условиях нестационарного сброса газа. Еще одним достоинством модели [11] является то, что появляется возможность использовать зависимость параметров атмосферы от времени, что особенно важно при моделировании продолжительных сбросов газа.
Предложенная модель может быть востребована для проведения анализа влияния конструктивных параметров на процесс истечения газа из свечи, что существенно при проектировании новых свеч и оптимизации режимных параметров при эксплуатации уже существующих. Так при проектировании свеч необходимо всегда исходить из того, что сброс газа должен оставаться безопасным даже в случае самых неблагоприятных метеоусловий. Для уже эксплуатируемых свеч первоочередную важность представляет определение расхода сброса, при котором концентрации на поверхности земли, а именно в местах размещения производственных объектов и в населенных пунктах, не будут превышать предельно допустимой концентрации (ПДК) или нижнего концентрационного предела распространения пламени (НКПРП) сбрасываемого газа, при любых классах устойчивости атмосферы.
Особенность выбора параметров атмосферного пограничного слоя.
В применяемых в настоящее время физико-математических моделях и методиках расчета сброса газа выбор параметров для численного моделирования осуществляется в несколько упрощенным способе. Например, в методике [13] масштаб длины Монина-Обухова, абсолютное значение которого определяет высоту, до которой влияние сил трения на турбулентность превышает влияние сил плавучести, находится с помощью коэффициентов, зависящих от класса устойчивости атмосферы и шероховатости поверхности. Данное обстоятельство существенно ограничивает возможности проведения расчетов с применением этой методики. Например, в случае одинакового рельефа местности при наличии температурной инверсии масштаб длины Монина-Обухова будет постоянной величиной и не будет зависеть от значений температуры и скорости потока. Это, в свою очередь, может существенно повлиять на значение скорости вовлечения окружающего воздуха вовнутрь облака и, следовательно, на описание распространение газа от места его выброса в окружающую среду.
Приближенные значения атмосферных параметров существенно могут повлиять на итоговые результаты расчета. Например, потенциально возможен вариант, при котором при неустойчивой стратификации атмосферы значения концентраций выбрасываемого газа не будут превышать значений ПДК и НКПРП на любых расстояниях от свечи; однако при инверсии и штиле, выброс с такой свечи уже может стать небезопасным, так как образующийся при этом газовоздушный шлейф будет прижиматься к поверхности земли.
С другой стороны в модели [9], в случае неизвестных профилей скорости ветрового потока, температуры и параметров турбулентности, вертикальные профили этих параметров определялись посредством проведения предварительных численных расчетов по следующему алгоритму. Сначала на входе задавались приблизительные значения интенсивности турбулентности It и масштаба турбулентности Mt (0.1 % и 0.1 м соответственно), а скорость ветра принималась постоянной по высоте. Далее вертикальные профили скорости и параметров турбулентности, полученные в выходном сечении расчетной области, использовались в качестве граничных профилей на входной границе, и расчет проводился заново.
Следует отметить, что в вышеупомянутой процедуре профили турбулентных характеристик k и ε (турбулентная кинетическая энергия и скорость диссипации турбулентной кинетической энергии) находились через выражения [14]:
| |
(1) |
где ![]() — средняя пульсационная скорость, а V – характерная скорость набегающего потока (в нашем случае это скорость ветра).
— средняя пульсационная скорость, а V – характерная скорость набегающего потока (в нашем случае это скорость ветра).
В уравнении переноса газа [9]:
| |
(2) |
коэффициент турбулентной диффузии ![]() (м2/с) определяется через отношение турбулентной вязкости
(м2/с) определяется через отношение турбулентной вязкости ![]() к турбулентному числу Шмидта
к турбулентному числу Шмидта ![]() :
:
| |
(3) |
В свою очередь, коэффициент турбулентной вязкости (кг/(м·с)) является функцией от плотности , турбулентной кинетической энергии k и скорости диссипации турбулентной кинетической энергии ε:
| |
(4) |
Перенос массы обусловлен турбулентной диффузией, и поскольку профиль коэффициента турбулентной диффузии в уравнении (2) при данном подходе [9] определяется через значения интенсивности и масштаба турбулентности, то основным недостатком данного подхода является не всегда адекватный учет вышеупомянутого профиля. В реальной действительности, интенсивность и масштаб турбулентности могут отличаться от используемых в модели значений. Отметим, что авторами процедуры [9], для более точного определения значений коэффициента турбулентной диффузии, предлагается использовать различные величины турбулентного числа Шмидта ![]() на основе привлечения экспериментальных данных.
на основе привлечения экспериментальных данных.
Одним из приемов для повышения точности расчетов является привлечение экспериментальных данных, снимаемых с метеодатчиков, которые могли бы использоваться в качестве граничных условий на входной границе в расчетной области для задания параметров атмосферного пограничного слоя с помощью UDF-функций [15]. Очевидно, что привлечение большего количества замеров параметров атмосферы по высоте приведет, в конечном счете, к более точным прогнозам распространения и рассеивания газа в атмосфере. Наиболее целесообразно выполнить замеры параметров атмосферы непосредственно на местности в момент сброса газа. Использование данных метеоизмерений предусмотрено в хорошо известном программно-аппаратном комплексе «Токси+Метео» [16]. Однако, несмотря на возможность автоматического включения метеопараметров в вычислительный процесс при помощи метеостанции, у этого подхода также имеются свои недостатки. Связаны они с тем, что комплекс «Токси+Метео» базируется на использовании интегральных законов сохранения, и, следовательно, в расчетах распространения опасного газа по этой методике невозможно учесть рельеф местности и наличие застройки. Для решения данной проблемы, учитывая необходимость оптимизации машинного расчетного времени и получение приемлемой точности конечных результатов, настоящим предлагается поэтапное применение метода градиента и метода профиля [17-18]. Эти методы применяются только для определения параметров атмосферного пограничного слоя. Нами предлагается применять их для получения профилей скорости и параметров турбулентности атмосферного воздуха при моделировании последствий сброса газа. Процедура поэтапного применения метода градиента и метода профиля следующая: используются показания метеодатчиков по скорости ветра и температуре воздуха. Затем с помощью метода градиента вычисляется масштаб длины Монина-Обухова для конкретной стратификации. На втором этапе с учетом найденного масштаба методом профиля определяются данные, необходимые для построения профилей скорости, температуры, значений k и ε: динамическая скорость, шероховатость, масштаб температуры, температура земли, средняя плотность воздуха и тепловой поток.
Ниже в качестве примера представлена процедура реализации этапов вычисления атмосферных параметров при наличии данных по температуре и скорости движения воздуха в 4 точках пространства по высоте. Рассматривается расчет параметров атмосферного пограничного слоя для устойчивой стратификации атмосферы (она является наиболее неблагоприятной). В вычислениях за основу взяты экспериментальные данные, приведенные в работе [19].
Этап I. Метод градиента.
Таблица 1 – Значения температуры Ti, и скорости ui в точках замера zi.
| zi, м | 2,5 | 5 | 7,5 | 10 |
| Устойчивая стратификация атмосферы | ||||
| Ti, К | 288,36 | 288,38 | 288,38 | 288,37 |
| ui, м/с | 3,69 | 4,33 | 4,72 | 5,00 |
На первой стадии находится среднегеометрические значения высоты между точками замеров (табл. 2).
Таблица 2 – Среднегеометрические высоты, ![]() , м.
, м.
| zmi, м | 3,54 | 6,12 | 8,66 |
Затем производится замена измеренной температуры в потенциальную температуру: ![]() К; где
К; где ![]() , К/м – адиабатический градиент температуры:
, К/м – адиабатический градиент температуры: ![]() ,
, ![]() — ускорение свободного падения м/с2, а
— ускорение свободного падения м/с2, а ![]() – удельная теплоемкость воздуха, Дж/(кг·К).
– удельная теплоемкость воздуха, Дж/(кг·К).
Таблица 3 – Значения потенциальной температуры ![]() ,
,
| zi, м | 2,5 | 5 | 7,5 | 10 |
| 288,38 | 288,43 | 288,45 | 288,47 |
Определим зависимость градиента изменений скорости и температуры, относительно среднегеометрических высот:
Число Ричардсона (критерий турбулентных процессов, протекающих в атмосфере) для первой среднегеометрической высоты будет равно:
Таблица 4 – Числа Ричардсона для всех среднегеометрических высот.
| zmi, м | 3,54 | 6,12 | 8,66 |
| Rim | 0,0090 | 0,0135 | 0,0155 |
С помощью чисел Ричардсона определяется масштаб длины Монина-Обухова:
Этап II. Метод профиля
Исходные данные те же, что и для метода градиента. Для нахождения динамической скорости и масштаба температуры используются графики, которые строятся в зависимости от класса устойчивости атмосферы:
- профиля скорости ui от функции масштаба длины Монина-Обухова ψi;
- профиля температуры Өi от функции масштаба длины Монина-Обухова ψi.
Таблица 5 – Значения функции масштаба длины Монина-Обухова для устойчивой атмосферы, ![]() [17-18].
[17-18].
| zi, м | 2,5 | 5 | 7,5 | 10 |
| ui, м/с | 3,69 | 4,33 | 4,72 | 5 |
| 288,38 | 288,43 | 288,45 | 288,47 | |
| ψi | 0,9448 | 1,6664 | 2,1004 | 2,4166 |
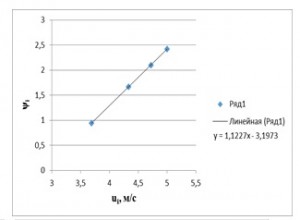
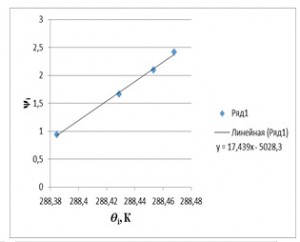
Для построения первого графика (рис. 1) наносятся точки с координатами (ui, ψi) и по ним строится график функции вида y=ax+b. Для построения второго графика (рис. 2) используют точки с другими координатами (, ψi). Здесь также составляется график функции вида y=ax+b.
Рис. 1. Зависимость скорости ui от функции масштаба длины Монина-Обухова ψi.
Рис. 2. Зависимость температуры Өi от функции масштаба длины Монина-Обухова ψi.
Из графика (рис. 1) функции вида y=ax+b определяется динамическую скорость ![]() и шероховатость
и шероховатость ![]() :
:
![]() = exp (-b) = exp (-3,197) = 0,04 м;
= exp (-b) = exp (-3,197) = 0,04 м;
где k – константа Кармана.
Аналогично с помощью графика (рис. 2) находится масштаб температуры ![]() и температура земли
и температура земли ![]() :
:
Используя, уже ставших известными, данные, вычисляется средняя плотность воздуха ![]() и тепловой поток
и тепловой поток ![]() :
:
![]() = 101325/(287,08·288,29) = 1,22 кг/м3,
= 101325/(287,08·288,29) = 1,22 кг/м3,
где ![]() – атмосферное давление, Па и
– атмосферное давление, Па и ![]() – универсальная газовая постоянная, Дж/(кг·К).
– универсальная газовая постоянная, Дж/(кг·К).
Стоит отметить, что в процессе определении атмосферных параметров возникает необходимость измерения значений температуры и скорости с точностью до десятичных и сотых, так как изменение параметров атмосферы по высоте незначительно. При неточных измерениях в случае нахождении чисел Ричардсона может быть получено либо искаженное значение масштаба длины Монина-Обухова, либо и вовсе значение с противоположным знаком, которое невольно поменяет в расчетах вид атмосферной стратификации.
Результаты расчетов
Применяемая физико-математическая модель была ранее верифицирована в работе [20] на основе экспериментальных данных при сбросе природного газа.
В качестве примера в выполненных расчетах сброса этилена со свечи (высота – 5 м, диаметр – 0,1 м) для устойчивой стратификации атмосферы задействованы граничные условия и параметры из представленного выше расчета поэтапного использования методов профиля и градиента. Характер распределения концентраций этилена рассчитывался и при нейтральной и неустойчивой стратификациях атмосферы, наряду с этим скорость ветра принималась равной 5 м/с на высоте 10 м. Непосредственно на оголовке свечи значения массового расхода (8,9 кг/с) и температуры этилена (273 К) во всех расчетах задавались идентично.
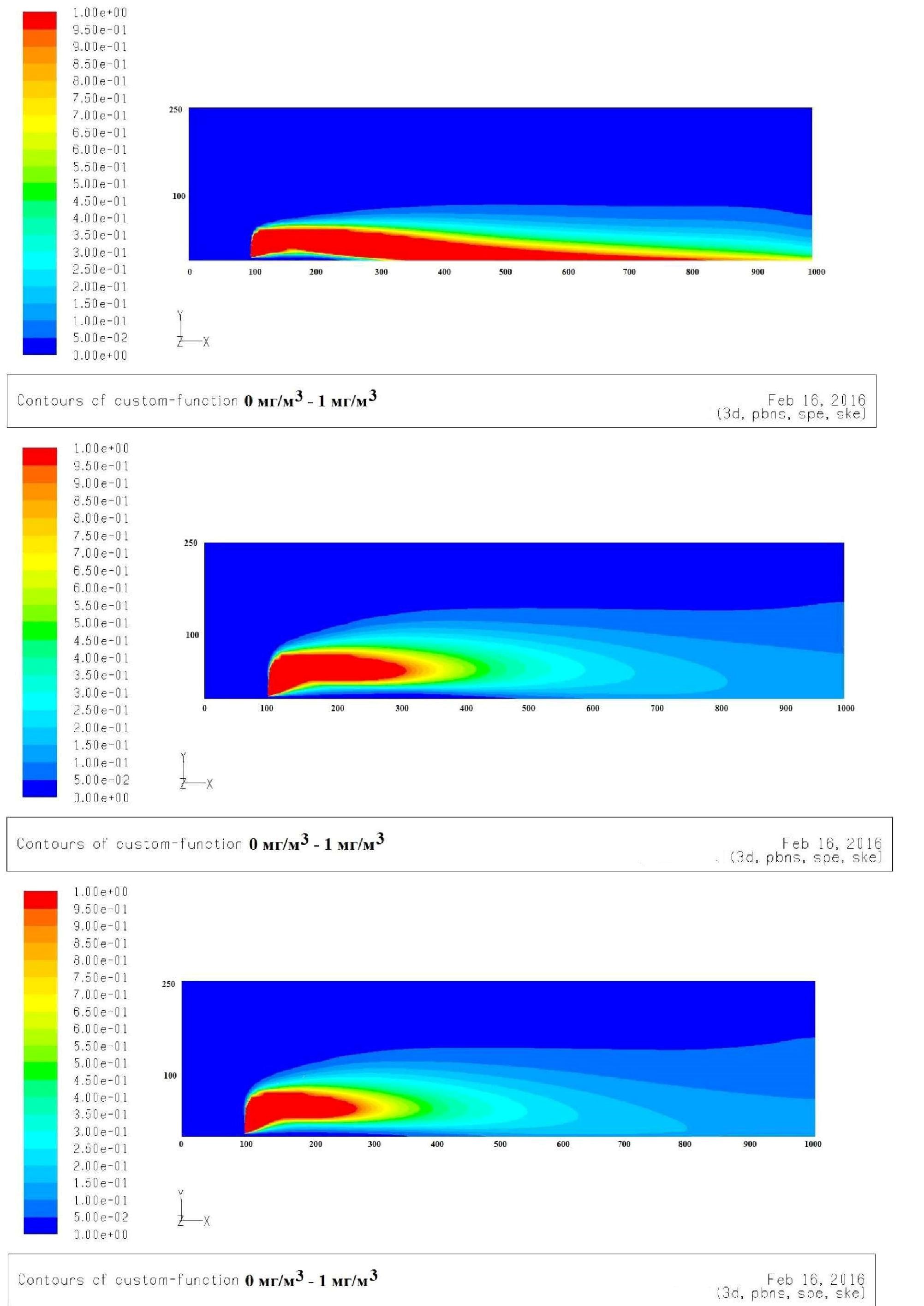
На рисунке 3 приведены расчетные изолинии (контуры) концентраций этилена (до 1 г/м3) при различных стратификациях атмосферы, вдоль оси направления ветра по центру газовоздушного облака. Свеча расположена на расстоянии 100 м от левой границы расчетной сетки. Из рисунков видно, что характер рассеивания этилена существенно зависит от условий устойчивости атмосферы. Для всех трех условий устойчивости атмосферы шлейф достигает поверхности земли, несмотря на значительный расход этилена со свечи и плавучесть легкого газа в воздухе. Как показали расчеты: наиболее опасным является сброс этилена через свечу в условиях устойчивой стратификации атмосферы. В этом случае значения концентраций в приземном слое оказываются намного выше по сравнению с другими рассматриваемыми устойчивостями атмосферы. Более того, на расстоянии с 250 до 800 м от свечи концентрация этилена в приземном слое начинает превышать предельно допустимую концентрацию (ПДК, равная 100 мг/м3) в 10 раз. При этом стоит акцентировать, что в условиях устойчивой стратификации газа преобладают нисходящие потоки воздуха, вследствие чего значительное количество этилена на определенном расстоянии начинает стелиться около земной поверхности.
Кроме того, результаты расчетов показали, что при других стратификациях атмосферы, начиная с 350 м от свечи по направлению ветра, концентрация этилена в приземном слое в 1,5 раза превышает ПДК. Заметно, что при нейтральной и неустойчивой стратификации наиболее опасные концентрации этилена, за счет воздушных потоков поднимаются вверх и тем самым не достигают земной поверхности. Дальнейший же рост концентрации, на расстоянии от свечи, например, при неустойчивости, вызван постепенным накапливанием газа, вследствие интенсивного перемешивания с воздухом при высокой турбулизации атмосферы.
Варьируя расходом, было установлено, что при расходе 2 кг/с, при неустойчивой и нейтральной стратификациях атмосферы на земной поверхности не образуются концентрации, превышающие ПДК. Таким образом, исключить аварийные ситуации можно благодаря сбросу опасного газа при ограниченном расходе и наиболее благоприятных метеоусловиях.
Рисунок 3 – Сброс этилена через свечу рассеивания: а) при устойчивой стратификации атмосферы; б) –при нейтральной стратификации атмосферы; в) – при неустойчивой стратификации атмосферы.
Заключение
На основе подхода поэтапного использования метода градиента и метода профиля, по нескольким (не менее трех) измерениям температуры воздуха и скорости ветра по высоте, расчетным путем можно получить параметры (масштабы Монина-Обухова и температуры, динамическую скорость, шероховатость и температуру земной поверхности, тепловой поток и плотность воздуха), описывающие характеристики пограничного атмосферного слоя. Полученные параметры используются для получения соответствующих профилей при моделировании распространения сброса через свечу газа в окружающую среду, позволяя корректно спрогнозировать характер распределения опасных концентраций.
Литература
- «Руководство по безопасности факельных систем». Утверждено приказом Ростехнадзора от 26.12.2012 № 779.
- Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. ОНД-86. Госкомгидромет. Общесоюзный нормативный документ, Л.: Гидрометеоиздат, 1987.
- Информационная бюллетень Ростехнадзора. Выпуск №32. 2007 год. URL:ib.safety.ru/assets/pdf/Bull_32 /Bull_32_32-41.pdf Обращение: 05.03.2015.
- Завгороднев А. В., Мельников А.В., Сафонов В.С. Проблема обеспечения безопасности сброса газа в атмосферу на объектах транспортирования и хранения природного газа. Безопасность труда в промышленности. 2011. №. 11. С. 66-71.
- Завгороднев А. В., Акопова Г.С., Толстова Н.С., Мельников А.В. Результаты исследований рассеивания в атмосфере организованных нестационарных выбросов газа на объектах газотранспортных предприятий. ТЕРРИТОРИЯ НЕФТЕГАЗ. 2011, № 12. С. 90-97.
- Купцов А.И., Акберов Р.Р., Исламхузин Д.Я., Гимранов Ф.М. Проблемы расчета рассеивания легких газов в атмосфере при их выбросах со свечи с учетом рельефа и застройки местности и атмосферной устойчивости / А.И. Купцов, Р.Р. Акберов, Д.Я. Исламхузин, Ф.М. Гимранов // Вестник Казанского технологического университета. – 2014. – № 6. – С. 284-286.
- Pontiggia M., Derudi M., Busini V., Rota R. Hazardous gas dispersion: a CFD model accounting for atmospheric stability class. Journal of Hazardous Materials. Vol. 171, №. 1. P. 739-747.
- Olav R. Hansen, Mathieu Ichard, Scott G. Davis. Validation of FLACS for Vapor Dispersion from LNG Spills: Model Evaluation Protocol // 12th Annual International Symposium of the Mary Kay O’Connor Process Safety Center, 27–28 Oct. 2009, Texas A&M University, College Station, Texas.
- Galeev A.D., Starovoitova E.V., Ponikarov S. I. Numerical simulation of the formation of a toxic cloud on outpouring ejection of liquefied chlorine to the atmosphere. Journal of Engineering Physics and Thermophysics. 2013. Vol. 86, No. 1. P. 219-228.
- Adel I. Kuptsov, Roald R. Akberov, Fidais M. Gimranov / Developing nomograms using CFD results for predicting propagation of hazardous gases released through vent stacks to the atmosphere // Contemporary Engineering Sciences, Vol. 9, 2016, no. 3, 113-124.
- Купцов А.И., Акберов Р.Р., Исламхузин Д.Я., Гимранов Ф.М. Численное моделирование пограничного слоя атмосферы с учетом ее стратификации. / А.И. Купцов, Р.Р. Акберов, Д.Я. Исламхузин, Ф.М. Гимранов // Фундаментальные исследования. – 2014. – № 9-7. – С. 1452-1460.
- Adel I. Kuptsov, Roald R. Akberov, Fidais M. Gimranov / Calculation of gas parameters at the exit from a gas vent stack by means of calculating duration of emptying of the processing equipment // Contemporary Engineering Sciences, Vol. 9, 2016, no. 3, 103-111.
- Руководство по безопасности «Методика моделирования распространения аварийных выбросов опасных веществ». Утверждено приказом Ростехнадзора от 20.04.2015 № 158.
- Снегирев А.Ю. Высокопроизводительные вычисления в технической физике. Численное моделирование турбулентных течений. СПб.: Изд-во Политехн. ун-та, 2009. – 143 с.
- Купцов А.И. «Экологический мониторинг. СFD-технологии. UDF-функции» / А.И. Купцов // Вестник технологического университета. – – № 20. – С. 203-207.
- Акопов А.А., Хлобыстова И.О., Марухленко С.Л., Марухленко А.Л., Софьин А.С. Программно-аппаратный комплекс «ТОКСИ+МЕТЕО» для оценки последствий возможных аварий с учетом данных о текущих погодных условиях. Безопасность труда в промышленности. 2011. №. 1. С. 22-25.
- Arya, S. P. Air Pollution Meteorology and Dispersion, New York: Oxford University Press, 1998.
- Arya, S.P. International Geophysics, ed. H. Holton, Academic Press, New York, 2001.
- Blackadar, A.K. 1997, Turbulence and Diffusion in the Atmosphere, Springer- Verlag, Berlin.
- Купцов А.И., Акберов Р.Р., Гимранов Ф.М. Влияние метеоусловий на динамику рассеивания опасного газа, сбрасываемого через технологические свечи. / А.И. Купцов, Р.Р. Акберов, Ф.М. Гимранов // Проблемы сбора, подготовки и транспорта нефти и нефтепродуктов. – 2015. – № 4 (102). – С. 171-177.
_____________________________________________________________
© А.И. Купцов – аспирант каф. промышленной безопасности КНИТУ, artpb@yandex.ru; Р.Р. Акберов — канд. техн. наук, доц. той же каф.; Ф.М. Гимранов — д-р. техн. наук, проф., зав. каф. промышленной безопасности КНИТУ; А. Г. Зубков – эксперт в области промышленной безопасности ООО «Эксперт-92», г. Казань.
© Kuptsov A.I. – postgraduate department of industrial safety KNRTU; artpb@yandex.ru; Akberov R.R. – candidate of technical sciences, associate professor department of industrial safety KNRTU; Gimranov F.M. — doctor of technical sciences, professor, head of industrial safety chair KNRTU, expert92@mail.ru; Zubkov A.G. – expert PLC «Expert-92», Kazan.