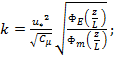Купцов А.И., Гимранов Ф.М. Численное моделирование сброса газов через свечу рассеивания на газотранспортных и газоперерабатывающих объектах // Журнал экологии и промышленной безопасности. — 2013. — Т. 59, № 3. — С. 16-17
УДК 622.691.2/.4.004.4
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ СБРОСА ГАЗОВ ЧЕРЕЗ
СВЕЧУ РАССЕИВАНИЯ НА ГАЗОТРАНСПОРТНЫХ
И ГАЗОПЕРЕРАБАТЫВАЮЩИХ ОБЪЕКТАХ
А.И. Купцов, аспирант кафедры ПБ, artpb@yandex.ru.
Ф.М. Гимранов, профессор, доктор технических наук.
ФГБОУ ВПО Казанский национальный исследовательский технологический университет
Для сбросов газов и паров при аварийных ситуациях путем рассеивания, а также при проведении плановых регламентных работ на технологическом оборудовании газотранспортных и газоперерабатывающих предприятиях используются специальные установки – свечи рассеивания. Как правило, свечи применяются при сбросе легких газов (метана, природного газа и водородсодержащего газа с отношением плотности газа к плотности воздуха не более 0,8). Такие сбросы в отдельных случаях могут быть настолько значительными, что могут служить причиной взрывов и пожаров.
Наибольшую опасность сбросы взрывоопасных газов представляют в тех случаях, когда вблизи места сброса находятся горящие факелы, оборудование с огневым обогревом (например, печи пиролиза, конверсии и т.д.) или другие постоянные источники поджигания. Поэтому при организации сбросов горючих и взрывоопасных газов и паров необходимо учитывать множество факторов: возможные максимальные объемы, физико-химические и взрывчатые свойства, условия их рассеивания и расстояния до источника воспламенения [1].
Помимо этого сбросы взрывоопасных газов и паров характеризуются сверхзвуковыми скоростями и нестационарностью процессов (расходы газа на начальных этапах стравливания и на конечных существенно различаются). Таким образом, учитывая сбросы в совокупности с метеорологическими факторами (состояние устойчивости атмосферы, скорость ветра, атмосферная диффузия и т.д.), возникает проблема правильной оценки пространственно-временного распределения сбрасываемого газа с учетом конструкционных характеристик свечи (диаметр, высота, скорость истечения и т.д.).
Для решения данной проблемы, как правило, применяют стационарные математические модели, известные как методика ОНД-86 [2], методика ВНИИГАЗ [3] и другие.
Перечисленные методики имеют ряд недостатков: фиксированные скорости истечения газа и параметры атмосферной диффузии при нестационарных режимах; отсутствие учета рельефа местности и размещения технологических объектов; отстутствие учета параметров метеоусловий и т.д.
В связи с этим наиболее эффективным для исследований процессов газодинамики считается численное моделирование, основанное на классических законах сохранения при помощи вычислительных комплексов. К таковым относится и программный комплекс Fluent. Данный комплекс был верифицирован в различных работах [4-5]. Это послужило главным аргументом для выбора его в качестве основного вычислительного инструмента.
Так как практически все процессы распространения в природе турбулентны, основным подходом к численному моделированию турбулентных рассеиваний является решение систем уравнений, осредненных по Рейнольдсу (Reynolds-averaged Navier-Stokes, RANS подход). Исходя из выше изложенного, в данной работе использовалась одна из самых распространенных моделей методики RANS-подхода: k-ε standard модель.
В качестве предварительного оценочного расчета был рассмотрен сброс природного газа (на 95% состоящего из метана) через свечу магистрального газопровода. Геометрические характеристики трубопровода и свечи магистрального газопровода (эффективный диаметр и высота) были взяты из экспериментальных исследований ОАО «Газпром» [6]. Рассматривался наиболее опасный класс стабильности по Паскуилу – F (инверсия) при сбросах газов в атмосферу, при этом скорость ветра на высоте 10 метров принималась за 1 м/с. Шероховатость поверхности (грунта) учитывалась как 1 см.
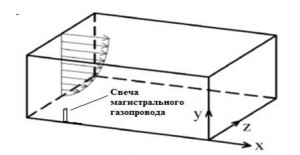
Граничные профили скорости, температуры и турбулентные характеристики на входе в расчетную область (рис. 1) определялись исходя из известных выражений [7-10]:
где u(z) – скорость ветра на высоте z; u* — динамическая скорость; K – константа Кармана (в расчетах использовалось значение 0,42); z0 – высота шероховатости; ![]() — универсальные безразмерные функции; L – масштаб длины Монина-Обухова; T(z) – температура на высоте z; T0 – температура поверхности (грунта); T* — масштаб температуры; g – ускорение свободного падения; cp – удельная теплоемкость при постоянном давлении; ε – скорость диссипации турбулентной кинетической энергии; k – турбулентная кинетическая энергия; cµ — коэффициент, равный 0,09.
— универсальные безразмерные функции; L – масштаб длины Монина-Обухова; T(z) – температура на высоте z; T0 – температура поверхности (грунта); T* — масштаб температуры; g – ускорение свободного падения; cp – удельная теплоемкость при постоянном давлении; ε – скорость диссипации турбулентной кинетической энергии; k – турбулентная кинетическая энергия; cµ — коэффициент, равный 0,09.
Масштаб длины Монина-Обухова рассчитывался как:
Температура на высоте 10 метров принималась равной 303К, а температура поверхности (грунта) равной 293К. Подставляя граничные и начальные условия, решалась система уравнений, состоящая из масштаба длины Монина-Обухова, а также из уравнений профилей ветра и температуры,
Затем подставляя найденные значения, находился тепловой поток:
где ρ – плотность.
Для учета инверсии в уравнении переноса скорости диссипации турбулентной кинетической энергии использовался источниковый член SЕ, непосредственно зависящий от универсальных безразмерных функций.
Рисунок 1. Расчетная область для численного моделирования сброса метана через свечу магистрального газопровода
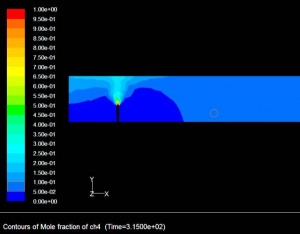
Результаты предварительного расчета приведены на рис. 2.
Рисунок 2. Расчетные изолинии концентраций метана после 315 секунд
стравливания метана через свечу магистрального газопровода.
Проведенный предварительный расчет показал, что стравливание газа (максимальный расход – 42 кг/с) через свечу магистрального трубопровода высотой 3,6 метра и диаметром 0,3 в случае инверсии не обеспечивает безопасность. Для обеспечения концентраций ниже НКПРП метана необходимы дополнительные исследования.
Список использованной литературы
- — Бесчастнов М, Соколов В. Предупреждение аварий в химических производ-ствах.Москва Машиностроение 1979г. 392 с.
- — ОНД 86Методика расчета концентраций в атмосферном воздухе вредных веществ содержащихся в выбросах предприятий. Госкомгидромет. Л.: Гидрометеоиздат, 1987. 68 с.
- — Методика расчета рассеивания газовых выбросов из наземных источников на объектах газовой промышленности. ВНИИГАЗ. 1987.
- — А.И. Купцов, Д.Я. Исламхузин, Ф.М. Гимранов, Экспериментальная установка для имитации процессов распространения облаков газов // Вестник Казан. технол. ун-та, 4, 229 — 231 (2013).
- — Т.Р. Тюменев. Дисс. канд. техн. наук, Казан. гос. технол. ун-т, Казань, 2008. 149 с.
- — Г.С. Акопова, С.В. Ганага, Н.С. Толстова. Проблемы моделирования рассеивания залповых выбросов загрязняющих веществ (природного газа) в атмосфере // Трубопроводный транспорт. Теория и практика. 2010. №1 (17).
- — Fluent Inc. Fluent 6.1. User’s Guide, Lebanon, 2003.
- — А.С. Монин «Теория турбулентности». Л.: Гидрометеиздат, 1987.
- — M. Pontiggia, M. Derudi, Rota. Hazardous gas dispersion: A CFD model accounting for atmospheric stability classes // Journal of Hazardous Materials 171 (1-3): 9 (2009)
- — H. Panofsky, J. Dutton. Atomospheric Turbulence, Wiley, New York, 1984. Atmospheric boundary layers. // Environ Modell Softw 23 (2008), 906-921