УДК 519.6
Ортина М.Н., Купцов А.И., Гимранов Ф.М.
«Математическое моделирование рассеивание облаков тяжелых газов
в условиях промышленной застройки: влияние метеоусловий».
— «Вестник технологического университета», №10 — 2017, с. 115-118
М.Н. Ортина, А.И. Купцов, Ф.М. Гимранов
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАССЕИВАНИЯ ОБЛАКОВ ТЯЖЕЛЫХ ГАЗОВ В УСЛОВИЯХ ПРОМЫШЛЕННОЙ ЗАСТРОЙКИ: ВЛИЯНИЕ МЕТЕОУСЛОВИЙ
PDF -полная версия статьи с формулами
Ключевые слова: математическое моделирование, тяжелые газы, промышленная застройка, метеоусловия.
Целью работы является исследование перемещения и рассеивания облаков тяжелых газов вблизи одиночного здания при различных скоростях ветра и условиях устойчивости. Использованная математическая модель основана на решении системы уравнений неразрывности, переноса импульса, энергии и газа с применением нестандартной k-ε модели турбулентности. Представлены результаты численного моделирования рассеивания тяжелого газа (смесь пропана (50%) с бутаном (50%)) вокруг препятствия кубической формы при нейтральных, устойчивых и неустойчивых условиях атмосферы. Для верификации результатов моделирования использованы экспериментальные данные, полученные на острове Торни [1]. Результаты численных расчетов согласуются с данными экспериментов.
Keywords: mathematical modeling, heavy gases, industrial area buildings, weather conditions.
The aim of this work is the researching of the transfer and dispersion of heavy gases clouds near a single building in different wind speeds and conditions of stability. The mathematical model is based on the solution of the system of equations of continuity, transfer of momentum, energy and gas using the non-standard k-ε model of turbulence. The results of numerical modeling of heavy gas dispersion (mixture of propane (50%) and butane (50%)) around the cubic obstacle in neutral, stable and unstable atmospheric conditions are presented. The experimental data, which were obtained on the Thorney Island, were used [1] to verify the simulation results. The results of the numerical calculations are consistent with the experimental data.
Введение
Объекты, на которых находятся и хранятся взрывоопасные газы, являются источниками повышенной опасности. Опасность таких объектов связана с возможным выбросом газа из оборудования при частичной разгерметизации или полном разрушении и, как следствие, с образованием взрывоопасных и/или токсичных облаков, способных перемещаться под действием ветра на значительные расстояния. Наибольшую опасность представляют «тяжелые газы» (плотность которых выше воздуха). Для них характерно «прижимание» к земной поверхности, и, соответственно, слабое рассеивание в атмосфере.
Как правило, в зоне распространения облака опасного газа могут находиться промышленные здания и сооружения. Можно предположить, что концентрация опасного газа в зоне препятствия будет зависеть от формы препятствия, расстояния от источника выброса до препятствия, от массы выброшенного газа, а также от атмосферных метеоусловий. Наличие препятствия существенно турбулизирует воздушные потоки. Все эти факторы могут оказывать значительное воздействие на процесс рассеивания облаков опасных газов. Непосредственно около здания или других препятствий шлейф тяжелого газа может завлекаться в теневую область здания относительно направления ветра, в результате чего распределение концентраций может сильно измениться. Может измениться и характер распространения облаков тяжелых газов в боковом и вертикальном направлениях вследствие сильного рециркуляционного движения внутри этой области.
Математическая модель
Основные уравнения.
При решении задач распространения опасных веществ в атмосферном воздухе используется система дифференциальных уравнений [2]:
1) Уравнение неразрывности:
∂ρ/∂t + ∂(〖ρu〗_i )/(∂x_i ) = 0; (1)
2) Уравнение переноса импульса:
∂(〖ρu〗_i )/∂t + ∂(〖ρu〗_i u_j )/(∂x_i ) = – ∂ρ/(∂x_i ) +
+ ∂ρ/(∂x_i ) [μ(〖∂u〗_i/〖∂x〗_j – 〖∂u〗_j/〖∂x〗_i – 2/3 δ_(ij ) 〖∂u〗_k/〖∂x〗_k )] ∂(ρ(u_i^,u_j^,) ̅ )/(∂x_i ) + ρg_i; (2)
3) Уравнение переноса энергии:
∂(ρh)/∂t + ∂(〖ρu〗_i h)/〖∂x〗_i = ∂/〖∂x〗_i (λ+ c_(p ) μ_t/〖Pr〗_t ) ∂T/〖∂x〗_i ; (3)
4) Уравнение переноса газа:
∂(ρY_S )/∂t + ∂(〖ρu〗_i Y_S )/〖∂x〗_i = ∂/〖∂x〗_i [(ρD+ μ_t/〖Sc〗_t ) (∂Y_S)/〖∂x〗_i ] (4)
Обозначения переменных, входящих в (1) — (4), соответствуют обозначениям в [2].
Выражение для турбулентной вязкости μ_t принимает вид (формула Колмогорова-Прандтля) [3]:
〖 μ〗_t= ρС_μ k^2/ε. (5)
Моделирование турбулентности. Выбор модели и граничных условий.
Одним из наиболее существенных недостатков стандартной k-ε модели является переоценка турбулентной кинетической энергии (ТКЭ) вблизи точек соударения потока о стенки препятствия или о другие твердые поверхности [4]. Неудовлетворительные численные прогнозы, выполняемые с применением стандартной k-ε модели, связаны с допущением, используемым в моделях вихревой вязкости для вычисления тензора касательных напряжений , и, следовательно, для вычисления генерации ТКЭ.
В связи с этим, в данной работе используется k-ε realizable модель турбулентности [5]. За счет использования другой формулировки (вводится улучшенный способ расчета турбулентной вязкости, а уравнение для скорости диссипации ТКЭ выводится из точного уравнения переноса среднеквадратичного значения пульсационного вихря скорости) модель лучше описывает подавления чрезмерной генерации ТКЭ в застойной зоне. Преимущество данной модели состоит в том, что она наиболее точно предсказывает распределение диссипации плоских и круглых струй, обеспечивает лучшее предсказание характеристик вращающихся потоков, пограничных слоев, подверженных сильным градиентам давления, отрывных течений, рециркуляционных течений и потоков, в которых существуют развитые вторичные течения.
Уравнения переноса турбулентных характеристик k-ε realizable модели:
∂/∂t (ρk)+ ∂/〖∂x〗_j (〖ρku〗_j )= ∂/〖∂x〗_j [(μ+ μ_t/σ_k ) ∂k/〖∂x〗_j ] +
+〖 P〗_k+ P_b- ρε- Y_M+S_k , (6)
∂/∂t (ρε)+ ∂/〖∂x〗_j (〖ρεu〗_j )= ∂/〖∂x〗_j [(μ+ μ_t/σ_ε ) ∂ε/〖∂x〗_j ]+
+〖ρC〗_1 Sε- ρC_2 ε^2/(k+ √vε)+C_1ε ε/k C_3ε P_b+S_ε , (7)
где
С1 = max [0.43,ŋ/(ŋ+5)], ŋ = Sk/ε, S = √(2S_ij S_ij )
В этих уравнениях P_k представляет формирование турбулентной кинетической энергии благодаря средним градиентам скорости, рассчитанных тем же путем, как и в стандартной k-ε модели. А P_b — формирование турбулентной кинетической энергии за счет плавучести, рассчитанной как и в стандартной k-ε модели.
В выражении (5) параметры определяются следующим образом:
C_(μ )= 1/(А_0+ А_(s ) 〖kU〗^*/ε) ; U* = √(S_ij S_ij+ Ω ̃_ij Ω ̃_ij ) ;
Ω ̃_ij 〖= Ω〗_(ij )- 2ε_ijk ω_k ; 〖 Ω〗_(ij )= Ω ̅_ij-ε_ijk ω_k,
где Ω ̅_ij – среднее арифметическое тензора скоростей вращения, рассматриваемого в системе отсчета, вращающейся с угловой скоростью〖 ω〗_k.
Константы А_0=4.04; А_(s )= √6 cosφ, где:
φ=1/3cos-1 (√6 W), W = (S_ij S_jk S_ki)/S ̃^3 , S ̃= √(S_ij S_ij ) ,
S_ij= 1/2 (〖∂u〗_j/〖∂x〗_i + 〖∂u〗_i/〖∂x〗_j ).
Константы k-ε realizable модели:
C1ε = 1.44; C2 = 1.9; σk=1.0; σε=1.2.
Для моделирования течения в пограничных слоях используют пристеночные функции. В работе была использована стандартная пристеночная функция (Standard Wall Functions), рекомендуемая к использованию с моделями семейства k-ε [6]. Она позволяет использовать крупные ячейки в пристеночной области, что экономит вычисли-тельные ресурсы.
В модели на верхней и боковых границах расчетной области использовалось граничное условие «Symmetry» (условие непроницаемости), означающее, что эти границы имеют нулевые градиенты переменных потока через них.
На выходе (правая граница) используется условие «Outflow» (Выход потока). Это граничное условие использовалось для моделирования границы выхода, так как распределение скорости по границе заранее не известно. Значения всех рассчитываемых величин экстраполируются из расчетной области.
На нижнюю границу (Wall – стенка) накладывается условие «прилипания или непроскальзывания» (No slip). Устанавливается величина эквивалентной шероховатости, полученная из выражения:
KS = (9.793 ∙ y_0)/C_S , (8)
где KS — эквивалентная высота элементов шероховатости на подстилающей поверхности, м; Cs – константа шероховатости = 0,5.
Для входной (левой) границы использовалось граничное условие «Velocity inlet» (скорость на входе), требующее задания профилей скорости, температуры, k и ε.
Эксперимент
Для проверки корректности расчетов с помощью выбранной математической модели использовались результаты эксперимента № 26, проведенного на острове Торни [1]. В ходе него инициировалось мгновенное разрушение аналога резервуара — цилиндрической конструкции (14 м в диаметре и 13 м в высоту) с выбросом смеси азота и фреона-12 по направлению ветра в сторону кубического препятствия (9м•9м•9м), помещенного на расстоянии 50 м от места выброса (рис. 1). Одновременно измерялись концентрации газа в двух разных точках: на высоте 6,4 м перед препятствием (с наветренной стороны) и на высоте 0,4 м на задней стороне препятствия (подветренной стороны).
Рис. 1. Эксперимент № 26 на острове Торни.
Ниже в табл.1 приведены значения концентраций смеси, полученные в ходе эксперимента. Затем они сравнивались со значениями, полученными с помощью математического моделирования. Необходимо отметить, что в целом наши вычисления и результаты, полученные иранскими исследователями [7], коррелируются с экспери-ментальными данными. При этом численные прогнозы хорошо согласуются с данными экспериментов в области перед зданием, чем вблизи задней стенки препятствия. Как правило, это связано с двумя основными причинами: не точное моделирование анизотропии, что приводит к тому, что турбулентный перенос во всех направлениях считается одинаково важным и влияние турбулентных потоков в основном и вертикальном направлениях оказывается завышенным, приводя к сглаживанию концентрационных градиентов; а также завышенные значения ТКЭ на наветренной стороне здания, которые могут привести к более сильному перемешиванию опасного газа до того, как он окажется втянутым в зону рециркуляции [8].
Таблица 1 – Время от начала эксперимента и значения концентраций смеси газов (% об.).
| Значения концентраций на высоте 6.4 м с наветренной стороны | Значения концентраций на высоте 0.4 м с подветренной стороны | |||
| Время (с) | Фреон-12 (% об.) |
Время (с) | Фреон-12 (% об.) |
|
| Эксперимент № 26 [1] | 10.00 | 4.715 | 22.30 | 2.124 |
| k-ε standard [7] | 22.43 | 5.542 | 58.02 | 2.161 |
| k-ε realizable [7] | 15.50 | 4.446 | 29.50 | 1.889 |
| k-ε realizable
|
18.00 | 4.683 | 37.5 | 2.119 |
Исследования
Проведенная верификация позволила нам использовать разработанную численную модель для дальнейших расчетов по рассеиванию облаков опасных газов.
Для изучения поведения облака тяжелых газов с помощью численного моделирования нами была выбрана пропан-бутановая смесь в соотношении 1:1. Значения предельно-допустимых концентраций (ПДК) и нижний концентрационный предел распространения пламени (НКПРП) этих газов [9-10] приведены в табл. 2.
Таблица 2 – Характеристика тяжелых газов.
| Пропан | Бутан | |
| Химическая формула | С3Н8 | С4Н10 |
| Молярная масса | 44.09 г/моль | 58.12 г/моль |
| ПДК | 300 мг/м3 | 300 мг/м3 |
| НКПРП | 1.7 % об.
31.0 г/м3 |
1.8 % об.
43.0 г/м3 |
Расчетная область (размер 150м*100м*40м) была разбита на 313722 ячейки. Смесь тяжелых газов, первоначально содержалась в резервуаре, а затем мгновенно освобождалась в присутствии кубического препятствия, расположенного на расстоянии 50 м по направлению ветра от места выброса. Расчетные концентрации газа вычислены на различных высотах в 27-ми точках: на передней, задней, верхней и боковых поверхностях здания, а также на расстоянии 5-ти метров от каждой из соответствующих сторон. Расчет проводился при различных метеоусловиях: учитывалась стратификация атмосферы, а также влияние скорости ветра (1 м/с, 2,5 м/с и 5 м/с).
Стратифицированный слой атмосферы моделировался с использованием UDF – функций [11] в качестве устойчивого, неустойчивого и нейтрального состояния атмосферы. В том случае, если вблизи поверхности земли температура воздуха ниже, чем в более высоких областях приземного слоя, то состояние атмосферы считается устойчивым (инверсия). Условия для вертикального распространения облака при этом ухудшаются. При неустойчивой атмосфере (конвекция) наблюдается вертикальное перемещение объемов воздуха (газа) и развитие турбулентности. В случае нейтральной стратификации атмосферы рассеяние примесей происходит с равной вероятностью, как по горизонтали, так и по вертикали.
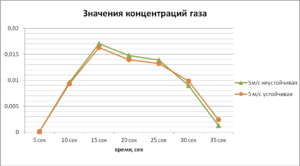
Результаты расчетов показали, что с начала рассеивания облака при конвекции концентрация выброшенного газа в области здания оказывается несколько выше, чем при инверсии. Это связано с тем, что значения турбулентных характеристик потока при неустойчивой атмосфере выше, и газ, перемешиваясь с воздухом, на первоначальном этапе быстрее рассеивается. Но примерно к 30-ой секунде значения концентраций при инверсии становятся выше и продолжают превышать значения концентраций, наблюдаемых при других состояниях атмосферы, до полного рассеивания газа в воздухе (рис. 2).
Однако следует отметить, что в целом состояние атмосферы не оказывало существенного влияния на значения концентраций газа: разница в значениях не превышала 5 %.
На поведение облака тяжелого газа в условиях застройки, главным образом, влияет ветер. Выявлена основная закономерность. Она заключается в том, что с увеличением скорости ветра возрастает турбулентность потока и, соответственно, уменьшается время рассеивания.
При набегании ветрового потока на препятствие происходит его торможение в продольном направлении и ускорение в поперечном, а также его восхождение и перемещение над зданием. Ветровой поток у поверхности земли около наветренной стороны здания переходит в пару вращающихся в противоположные стороны вихрей в следе здания. С подветренной, наветренной стороны здания и на крыше, в результате отрыва потока, образуются рециркуляционные зоны. Необходимо отметить, что в рециркуляционной зоне с подветренной стороны здания значения концентраций газа даже при больших скоростях ветра не достигают опасных значений. Облако тяжелого газа, содержащее в себе высокие концентрации, проходя вдоль боковых поверхностей препятствия, слабо втягивается в зону рециркуляции у подветренной стороны из-за высокой плотности. В результате, оно разделяется препятствием на две части и продолжает относиться вдоль по направлению ветра, при этом опасные концентрации газа остаются сосредоточенными по правую и левую сторону от здания (рис.3).
Рис. 2. Концентрации газа (% об.) при скорости ветра
5 м/с на расстоянии 5 м от наветренной стороны препятствия на высоте 4.5 м
Рис. 3. Концентрация газа (% об.) через 35 секунд от начала рассеивания при скорости ветра 5 м/с и устойчивом состоянии атмосферы
Заключение
Количественные показатели рассеивания опасного газа, полученные в результате численного моделирования с помощью модели турбулентности k-ε realizable, вполне приемлемо согласуются с экспериментом № 26 на острове Торни.
Результаты моделирования рассеивания смеси тяжелых газов показали, что основным фактором, влияющим на распространение облака, является скорость ветра. При этом в ходе исследования зона у подветренной стороны здания оказалась менее опасной по сравнению с областью у передней и боковых сторон строения.
Стратификация атмосферы не существенно влияет на рассеивание тяжелого газа в отличие от скорости ветра. Однако важным является вывод, что в начальный момент времени (до 25-30 сек) концентрации газа вследствие высокой турбулентности оказываются выше при неустойчивой атмосфере, а скорость убыли концентрации облака газа — ниже при устойчивом состоянии атмосферы.
Литература
1. Davies M. E., Singh S. The Phase II Trials: A data set the effect of obstructions // Journal of Hazardous Materials. – 1985. – v.11. – pp. 301-323.
2. Галеев А.Д. Образование и распространение облаков тяжелых газов при авариях на объектах химической и нефтехимической промышленности: Дис….канд. техн. наук: 05.26.03 / Галеев Айнур Дамирович. — Казань, 2006. — 227 с.
3. Снегирёв А.Ю. Высокопроизводительные вычисления в технической физике. Численное моделирование турбулентных течений: Учеб. пособие. СПб.: Изд-во Политехн. ун-та, 2009. — 143 с.
4. Lien, F.S., Yee, E., 2004. Numerical modelling of the turbulent flow developing within and over a 3-D building array, part I: a high-resolution Reynolds-averaged Navier–Stokes approach. Boundary-Layer Meteorology 112, 427–466.
5. Shih T.-H., Liou W. W., Shabbir A., Yang Z., Zhu J. A New k-ε Eddy-Viscosity Model for High Reynolds Number Turbulent Flows – Model Development and Validation // Computers and Fluids. 1995. Vol. 24 No 3. P. 227-238.
6. Батурин О.В. Расчет течений жидкостей и газов с помощью универсального программного комплекса Fluent. Учеб. пособие / О.В. Батурин, Н.В. Батурин, В.Н. Матвеев – Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2009. – 151 с.
7. Tauseef S.M., D. Rashtchian D.R., Abbasi S.A. CFD-based simulation of dense gas dispersion in presence of obstacles // Journal of Loss Prevention in the Process Industries. – 2011. — №24. – рр. 371-376.
8. Santos J.M., Reis Jr. N.C., Goulatr E.V. and Mavroidis I. ¬¬Numerical simulation of flow and dispersion around an isolated cubical building: The effect of the atmospheric stratification // Atmospheric Environment. – 2009. – №43. – pp. 5484–5492
9. ГОСТ 12.1.007-76 Система стандартов безопасности труда (ССБТ). Вредные вещества. Классификация и общие требования безопасности.
10. ГН 2.2.5 1313-03. Гигиенические нормативы «Предельно допустимые концентрации (ПДК) вредных веществ в воздухе рабочей зоны». Утверждены Главным государственным санитарным врачом Российской Федерации, Первым заместителем Министра здравоохранения Российской Федерации 27 апреля 2003 г. Введены в действие Постановлением Главного государственного санитарного врача Российской Федерации от 30.04.03, №76 с 15 июня 2003 г. – 16 с.
11. А. И. Купцов. Экологический мониторинг. CFD-технологии. UDF-функции. Вестник технологического университета. 2015. Т.18, №20. – С. 203-206.
_________________________________________________________________________
© М. Н. Ортина – магистрант каф. промышленной безопасности КНИТУ; А. И. Купцов – канд. техн. наук, инженер каф. промышленной безопасности КНИТУ, [email protected]; Ф. М. Гимранов – д-р техн. наук, проф., зав. каф. промышленной безопасности КНИТУ, [email protected], г. Казань.
© M. N. Ortina — graduate student department of industrial safety KNRTU; A. I. Kuptsov – candidate of technical sciences, engineer department of industrial safety KNRTU, [email protected]; F. M. Gimranov — doctor of technical sciences, professor, head of industrial safety chair KNRTU, [email protected], Kazan.



Свежие комментарии