Купцов А.И., Гимранов Ф.М. «Применение искусственных нейронных сетей для прогнозирования интенсивности испарения аварийной жидкости с поверхности пролива». — «Вестник технологического университета», №24 — 2016, с. 113-117.
УДК 004.942, 614.83
Купцов А.И., Гимранов Ф.М.
ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ ИНТЕНСИВНОСТИ ИСПАРЕНИЯ АВАРИЙНОЙ ЖИДКОСТИ С ПОВЕРХНОСТИ ПРОЛИВА
Ключевые слова: испарение с поверхности пролива, нейронные сети, достоверность расчетов.
С использованием математического аппарата искусственных нейронных сетей вычислены интенсивности испарения этанола, циклогексана и сжиженного бутана. Проведено сравнение результатов расчета интенсивности испарения по вычислениям нейросетевой и численной моделей с экспериментальными данными.
Keywords: pool evaporation, artificial neural network, model validation.
Using artificial neural networks predicted the intensity of evaporation of ethanol, cyclohexane and liquefied butane. A comparison of the calculation results of intensity of evaporation is projected neural networks and computing numerical simulation with experimental data.
Полная версия с формулами представлена здесь.
Введение
Одним из наиболее распространенных сценариев аварий на химических предприятиях является разгерметизация технологического оборудования с последующим образованием проливов токсичной и/или взрывоопасной жидкости. Для корректной оценки потенциальной опасности подобного сценария немаловажную роль играет определение значений интенсивности испарения аварийной жидкости с поверхности пролива. В частности, данная величина позволяет определить какое количество вещества испарится с поверхности аварийного пролива. В настоящее время с целью ее нахождения применяются как полуэмпирические уравнения, так и модели вычислительной гидродинамики (CFD) [1-13].
Ряд полуэмпирических математических методов по определению интенсивности испарения рассмотрен в работе [1]. Как правило, полуэмпирические модели, основанные на корреляции соответствующих экспериментальных данных, точно предсказывают только те показатели, которые были использованы при верификации проводимых исследований. В качестве ключевого параметра для выбора наиболее приемлемой модели, предлагается использовать значения скорости воздушного потока над аварийным проливом. Так, при отсутствии подвижности воздуха (например, в невентилируемом помещении) рекомендуется пользоваться моделью Mackay и van Wesembeeck [2]; а когда скорость ветра превышает 1 м/с хорошее совпадение обеспечивает модель, описанная Heymes и др. [3]. При этом, следует отметить, что ни одна из указанных полуэмпирических моделей не способна спрогнозировать массовый поток или интенсивность испарения с погрешностью меньше, чем 30%.
Использование моделей вычислительной гидродинамики позволяет преодолеть ограничения существующих полуэмпирических моделей. Данный подход, основанный на решении трехмерных уравнений сохранения массы, импульса и энергии, показывает в большинстве случаев хорошее согласование с экспериментальными данными по испарению веществ [4-13]. Однако, использование пакетных программ CFD для вычислений требуют доработки, в частности, по определению источников и стоков тепла, поведения жидкости, условий на границе раздела [10]. Кроме того, известно, что подобные программы обладают большой стоимостью, требуют высококвалифицированных специалистов, а время расчета одного варианта может занимать от нескольких часов до нескольких недель, что не всегда приемлемо, особенно в тех случаях, когда требуется оперативная оценка последствий аварии для принятия экстренных мер по их локализации и ликвидации.
Оперативное прогнозирование с учетом влияющих на испарение факторов и повышение точности прогноза может быть достигнуто путем применения нетрадиционных подходов и методов, таких, например, как методы искусственного интеллекта. В настоящее время в практике математического моделирования используются искусственные нейронные сети (ИНС), которые позволяют эффективно решать практические задачи экологии и промышленной безопасности [14-17]. Анализ подобного ряда работ показал, что ИНС позволяют значительно проще получать сопоставимые по точности результаты, чем расчетные и вычислительные методики, а также дают возможность учесть дополнительные факторы.
В данной статье проведено сравнение результатов расчетов по нахождению массового потока и интенсивности испарения с помощью нейросетевой модели с данными экспериментов по испарению этанола [4], циклогексана [18] и сжиженного бутана [19], а также с данными, полученными с помощью модели вычислительной гидродинамики.
Искусственная нейронная сеть
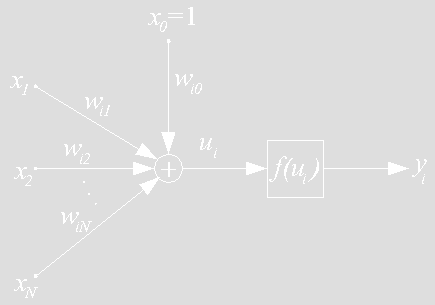
Применение алгоритмов, имитирующих процессы поведения реальной природной нервной клетки, позволяет проводить «обучение» ИНС. Модель i—нейрона можно представить в виде схемы (рис. 1).
Рис. 1. Обобщенная структурная схема
искусственного нейрона
Здесь — вектор входных сигналов нейрона, а — константный «псевдосигнал», сигнал поляризации (поляризатор). В общем случае, относится к действительным числам, во многих моделях они дискретны и могут принимать значения из множества {0,1} или {-1,1}, однако в некоторых реализациях используются как комплексные числа.
Вес для размерного входного сигнала имеет обратную к нему размерность. Например, если имеет размерность [кг/с], то размерность — [c/кг].
Взвешенная сумма входных сигналов служит аргументом функции активации искусственных нейронов , которая, в свою очередь, определяет значение выходного сигнала . Если значение функции превышает некоторый заранее определенный порог, то нейрон активирован и передает импульс следующим нейронам в сети. Существует множество различных функций, используемых в качестве активационных. Выбор ее вида является сложной задачей. Как правило, к ним выдвигаются требования иметь область значения [0,1] или [-1,1] и быть возрастающими. Примеры таких функций: сигнум, сигмоид. Иногда выдвигают дополнительное требование дифференцируемости.
Объединенные (путем передачи сигналов) между собой нейроны и образуют ИНС.
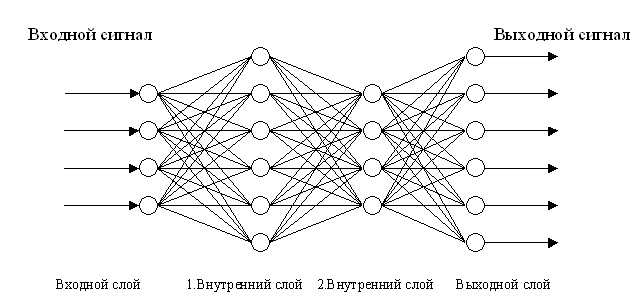
В простейших однослойных ИНС входные сигналы нейрона являются входными сигналами сети, а выходные сигналы нейрона – выходными сигналами сети. В многослойных сетях (рис. 2) роль входных сигналов некоторых нейронов играют выходные сигналы предыдущих слоев ИНС.
Рис. 2. Пример схемы многослойной ИНС
с двумя внутренними слоями
ИНС способна обучаться решению задач, для которых не существует быстрых или работающих с приемлемой точностью теоретических или эмпирических алгоритмов. Наряду с обучающими данными требуется лишь задать некоторый критерий качества решения задачи, который сеть при своём обучении должна будет минимизировать или оптимизировать [20-21].
Результаты расчетов
Для проверки адекватности нейросетевой модели было проведено сравнение вычисленных результатов с экспериментальными данными [4, 18-19]. Эксперименты по испарению этанола и циклогексана проводились на открытом воздухе при постоянных температурах, как на ровной, так и на сильно шероховатой поверхности. Поддон для пролива имел диаметр 0,74 м и был изолирован от грунта.
При обучении ИНС входными полями совместно служили параметры экспериментов как по испарению этанола, так и циклогексана (температура поверхности, скорость ветра на высоте 2 м, шероховатость, плотность вещества). Выходным полем являлись искомые данные массового потока.
Авторами ИНС реализованы на языке Python при помощи библиотеки PyBrain [22]. Нормализация входных сигналов задавалась как линейная, тогда как у выходного сигнала она оставалось нелинейной. Функцией активации являлся сигмоид с параметром, равный единице. Внутри каждой ИНС использовался один скрытый слой с 10 нейронами. Для обучения сетей использовалось 90% выборки. Во избежание ошибок скорость обучения сети была задана как 0,1. Количество итераций во время обучения не превышало 100 000. Время обучения ИНС составляло в среднем 1 минуту, что, в конечном счете, является весомым преимуществом использования сетей перед моделями CFD при срочной оценке последствий аварии.
Процедура получения результатов (кросс-валидация) заключалась в том, что после каждого обучения ИНС, на вход подавались входные сигналы в виде параметров эксперимента, который для сети в процессе обучения был неизвестен; после чего сеть выдавала выходной сигнал.
Ниже в таблице приведены экспериментальные данные и расчетные значения по испарению этанола и циклогексана при различных температурах и скоростях ветра. Вычисленные значения с помощью нейросети по сравнению с численной модели CFD [13] точнее и значительно быстрее прогнозируют результаты экспериментальных данных. Значения, полученные ИНС, имеют разницу δ к результатам измерений от 0,18 до 24,31% со средним значением 5,94%; тогда как у численной модели разница δ от 0,6 до 47,4% со средним значением 12,69%.
Таблица 1 – Экспериментальные данные и вычисленные значения по испарению этанола и циклогексана.
| № | Tliq, K | U[1], м/с
|
Массовый поток Jg,s, г/с | ||
| Эксперимент | CFD [13] | ИНС | |||
| Этанол | |||||
| Ровная поверхность (шероховатость – 0,0002 м) | |||||
| 1 | 310,15 | 1,4 | 0,456 | 0,393 | 0,461 |
| 2 | 309,65 | 1,9 | 0,533 | 0,523 | 0,532 |
| 3 | 325,15 | 1,7 | 1,02 | 1,06 | 1,10 |
| Сильно шероховатая поверхность (0,04 м) | |||||
| 4 | 305,65 | 1,4 | 0,488 | 0,536 | 0,437 |
| 5 | 310,15 | 1,8 | 0,679 | 0,9 | 0,69 |
| 6 | 324,65 | 1,8 | 1,32 | 1,96 | 1,641 |
| Циклогексан | |||||
| Ровная поверхность (шероховатость – 0,0002 м) | |||||
| 7 | 303 | 2,71 | 1,08 | 1,11 | 1,055 |
| 8 | 310 | 3,05 | 1,63 | 1,66 | 1,731 |
| 9 | 317 | 3,49 | 2,33 | 2,55 | 2,121 |
| Сильно шероховатая поверхность (0,04 м) | |||||
| 10 | 303 | 1,71 | 0,967 | 1,15 | 1,009 |
| 11 | 310 | 1,62 | 1,35 | 1,46 | 1,307 |
| 12 | 317 | 1,4 | 1,67 | 1,68 | 1,66 |
Другие эксперименты, например, с жидким бутаном [19], находившимся в теплоизолированном поддоне при температуре ниже температуры кипения, также представляют практический интерес для сравнения численной модели [9] с нейросетевой.
По практическим соображениям в расчетах с жидким бутаном была оставлена та же архитектура ИНС, которая описывалось выше. Входными сигналами послужили температура воздуха, температура жидкости и скорость ветра на высоте 9,15 м. Однако, при вычислениях нескольких экспериментов диапазон нормализации для температур и скорости ветра был увеличен. В противном случае сеть обучалась бы лишь в диапазонах параметров известных экспериментов, и при резко отличающемся входном сигнале выдавала бы статистическую ошибку. Так, например, в ходе подобных расчетов велика вероятность получить интенсивность испарения со знаком минус (сток), что абсолютно противоречит физике процесса.
Результаты расчетов и экспериментальные приведены в табл. 2.
Таблица 2 – Экспериментальные и расчетные значения по интенсивности испарения сжиженного бутана
| № | Tвоз, K | Tж, K | U[2], м/с
|
Интенсивность испарения, кг/(м2∙с) | ||
| Эксперимент | CFD [9] | ИНС | ||||
| 1 | 283 | 236,6 | 3,5 | 0,0037 | 0,0032 | 0,0035 |
| 2 | 282 | 241 | 3,0 | 0,0027 | 0,0035 | 0,0035 |
| 3 | 280 | 244,2 | 1,5 | 0,0023 | 0,002 | 0,0014 |
| 4 | 291 | 247,8 | 3,6 | 0,0046 | 0,0027 | 0,0051 |
| 5 | 289 | 237,6 | 5,8 | 0,0061 | 0,0045 | 0,0063 |
| 6 | 275 | 238,8 | 5,5 | 0,0056 | 0,0064 | 0,0051 |
| 7 | 287 | 236 | 6,9 | 0,0072 | 0,0066 | 0,006 |
| 8 | 282 | 263 | 1,0 | 0,002 | 0,0037 | 0,0015 |
Экспериментальное значение интенсивности испарения в опыте №8 почти в 2 раза меньше (85% отклонения) по сравнению с расчетом по модели CFD. Полученное расхождение авторы работы [9] обусловливают неопределенностью информации о метеорологических условиях (отсутствие детальной информации относительно степени устойчивости атмосферы). Вместе с тем, ИНС прогнозирует этот эксперимент с расхождением в 25%. При нахождении среднего значения разницы δ к результатам измерений, эксперимент № 8 не учитывался, так как метеоусловия действительно могут сильно влиять на результаты численной модели [23]. Но несмотря на это, вычисленные значения по CFD модели с разницей δ к экспериментальным данным от 13,04 до 41,3% со средним значением 18,29% уступают полученным по ИНС. Значения по ИНС получены с разницей δ к результатам измерений от 5,41 до 39,13% со средним значением 14,24%.
Заключение
ИНС позволяют за кратчайшие сроки спрогнозировать базовые характеристики испарения аварийной жидкости: интенсивность и/или массовый поток, и тем самым произвести корректную оценку потенциальной опасности испарения пролива. Результаты, полученные с помощью нейросетевой модели, хорошо согласуются с экспериментальными данными и превосходят вычисления с помощью численных моделей. При этом расчеты на ИНС можно улучшить, меняя архитектуру сети (добавление нейронов, скрытого слоя, варьирование видом функции активации и т.д.), увеличивая или уменьшая диапазон нормализации, а также используя дополнительные параметры испарения в качестве входных сигналов.
Очевиден и главный недостаток сетей перед численными и полуэмпирическими моделями – они не смогут спрогнозировать интенсивность испарения без «обучающей» выборки. Следовательно, требуется проведение большого количества экспериментов с разными веществами и диаметром пролива. Однако, учитывая дороговизну подобных исследований, их могли бы заменить расчеты по численной модели. Тогда подобный «симбиоз» моделей позволил бы при любых обстоятельствах оперативно решать практические задачи экологии и промышленной безопасности.
Литература
- Mazzarotta B., Bubbico R., 2016, Predicting evaporation rates from pools, Chemical Engineering Transactions, 48, 49-54
- Mackay, D., van Wesenbeeck, I., 2014, Correlation of chemical evaporation rate with vapour pressure, Env. Science & Tech., 48, 10259-10263
- Heymes, F., Aprin, L., Bony, A., Forestier, S., Cirocchi, S., Dusserre, G., 2013, An experimental investigation of evaporation rates for different volatile organic compounds, Proc. Safety Prog., 1-6.
- Habib, A., Schalau, B., Acikalin, A., & Steinbach, J. (2009). Transient calculation of the boundary layer flow over spills. Chem. Eng. Technol., 32, 306–311.
- Rong, L., Nielsen, P.V., & Zhang, G.Q. (2010). Experimental and numerical study on effects of airflow and aqueous ammonium solution temperature on ammonia mass transfer coefficient. J. Air Waste Manag. Assoc., 60, 419–428.
- Rong, L., Elhadidi, B., Khalifa, H.E., Nielsen, P.V., & Zhang, G.Q. (2011). Validation of CFD simulation for ammonia emissions from an aqueous solution. Comput. Electron. Agric., 75, 261–271.
- Saha, C. K., Wu, W., Zhang, G., & Bjerg, B. (2011). Assessing effect of wind tunnel sizes on air velocity and concentration boundary layers and on ammonia emission estimation using computational fluid dynamics (CFD). Comput. Agric, 78, 49–60.
- Vik, T., & Pettersson Reif, B.A. (2011). Implementation of a new and improved evaporation model in Fluent, FFI-rapport 2011/00116, Norwegian Defence Research Establishment (FFI).
- Старовойтова Е.В., Галеев А.Д., Поникаров С.И. Моделирование парообразования с поверхности аварийного пролива сжиженного газа // Вестник Казанского технологического университета. – 2012. – № 4. – С. 110-112.
- Галеев А.Д., Дьяконов Г.С., Поникаров С.И., Салин А.А. Испарение аварийно химически опасных веществ из проливов при авариях на ОПО // Вестник Казанского технологического университета. – 2014. – № 24. – С. 238-241.
- Raimundo, A.M., Gaspar, A.R., Oliveira, A.V.M., & Quintela, D.A. (2014). Wind tunnel measurements and numerical simulations of water evaporation in forced convection airflow. Int. Thermal Sciences, 86, 28–40.
- Galeev, A.D., Salin, A.A., Ponikarov, S.I. (2015). Numerical simulation of evaporation of volatile liquids, Journal of Loss Prevention in the Process Industries, 38, 39-49.
- Старовойтова Е.В., Галеев А.Д., Поникаров С.И. Сравнительный анализ подходов для расчета интенсивности испарения с поверхности аварийного пролива // Вестник Казанского технологического университета. – 2016. – № 8. – С. 116-118.
- Дударов С.П., Папаев П.Л., Кудряшов А.Н., Карибова Ю.А. Ячеечно-нейросетевые модели в задачах экологической безопасности // Искусственный интеллект и принятие решений. — 2011. — № 2. — С. 31–39.
- Новиков В.В., Мартыненко А.А., Солонникова Н.В. Экспресс-оценка риска на предприятиях машиностроения методами нейронных сетей // Вестник ДГТУ. – 2013. – № 3-4. – С. 82– 90.
- Потылицына Е.Н., Липинский Л.В., Сугак Е.В. Использование искусственных нейронных сетей для решения прикладных экологических задач // Современные проблемы науки и образования. – 2013. – № 4. – С. 1– 8.
- Королев, Д.С. Прогнозирование пожароопасных свойств веществ и материалов с использованием дескрипторов и искусственных нейронных сетей // Научно-теоретический журнал «Вестник БГТУ им. В.Г. Шухова». – 2015. – № 4. – С. 100– 103.
- Khajehnajafi S., Pourdarvish R. (2011). Correlations for mass transfer from a liquid spill: Comparisons and recommendations. Process Saf. Prog., 30, 178–184.
- Brighton, P.W.M. Further verification of a theory for mass and heat transfer from evaporating pools // Journal of Hazardous Materials. — 1990. — No 23. —pp. 215-234.
- Круг П.Г. Нейронные сети и нейрокомпьютеры: Учебное пособие по курсу «Микропроцессоры». – М.: Издательство МЭИ, 2002. – 176 с.
- Спицын В.Г., Цой Ю.Р. Применение искусственных нейронных сетей для обработки информации: методические указания к выполнению лабораторных работ. – Томск: Изд-во Томского политехнического университета, 2008. – 31 с.
- URL: http://pybrain.org/ (дата обращения: 01.06.2016)
- Купцов А.И., Акберов Р.Р., Гимранов Ф.М. Влияние метеоусловий на динамику рассеивания опасного газа, сбрасываемого через технологические свечи // Проблемы сбора, подготовки и транспорта нефти и нефтепродуктов. – 2015. – № 4. – С. 171-177.
_________________________________________________________________________
© А.И. Купцов – аспирант каф. промышленной безопасности КНИТУ, artpb@yandex.ru; Ф.М. Гимранов — д-р. техн. наук, проф., зав. каф. промышленной безопасности КНИТУ.
© Kuptsov A.I. – postgraduate department of industrial safety KNRTU; artpb@yandex.ru; Gimranov F.M. — doctor of technical sciences, professor, head of industrial safety chair KNRTU, expert92@mail.ru.
[1] U, м/с – скорость ветра на высоте 2 м
[2] U, м/с – скорость ветра на высоте 9,15 м